摘要： 在五金模具设计中，有时会涉及到一些比较复杂形体的翻边尺寸计算问题，作为模具设计人员，这些计算在模具设计过程中也是非常重要的内容之一。本文将介绍几种比较复杂形体翻边的计算方法，并相应介绍了计算原理与计算公式等。

关键词： 五金模具设计，翻边，计算原理与计算公式，复杂形体

Research of Calculative Methods for the Complicated

Draw-hole Sizes in the Design of Dies

Faculty of Mold & Die Engineering, Ningbo Polytechnic, Huang Yi-jun, Ningbo, Zhejiang, China, 315800

Abstract:  It might be sometimes deal with the calculation of the more complicated draw-hole sizes ，as the designers of dies, that is one of the very important contents in design of dies. The article will introduce several complicated methods of calculation and the principle as well as formula and so on.

Key Words:  Design of Dies, Draw-hole, Calculative principle & Formula, Complicated shapes

1  引言

    五金模具是模具类别中应用最广泛的一种。五金模具的设计过程本身就是一项技术性与工艺性紧密结合的工作过程，金属材料在冷五金模具的作用下，将变成一定形状、尺寸和性能的金属零件。

翻边（孔）的成形过程是一种模具成形的典型工艺过程，同时，翻边（孔）的尺寸与模具的设计尺寸有着直接的关系，所以设计计算是非常重要的环节之一。

2  应用实例、计算原理与计算公式

2.1  圆形翻边的应用实例

圆形翻边的应用实例如图1所示。

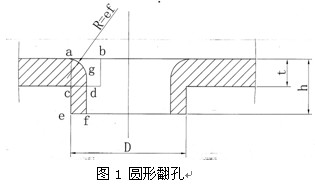
2.1.1圆形翻边的计算原理与计算方法

原理：圆形翻边的尺寸计算原理根据体积不变原理,即翻边前后材料体积不变,在图1中,abcd四边形面积=gfea所围成的实体面积,即翻边前由abcd所围成的面积等于翻边后gfea所围成的实体面积，其中ac=bd=t（材料厚度）。

在翻边高度不深的情况下，h=3P（P为螺纹距离,即保证翻出边的高度等于3倍螺纹螺距），R=ef（即翻边内圆相切弧半径R等于翻边后孔的壁厚ef），见图1所示。

2.1.2圆形翻边的计算公式

因为                t ×ab  = （h-ef）× ef + π × （ef）²/ 4

所以                ab = ｛h ×ef + （π/4-1）×ef ² ｝/t

其中，t ×ab 的乘积为翻边前图示实体截面积，

（h-ef）×ef为翻边后图1中由cdef所围成的实体截面积，

π × （ef）²/ 4为翻边后1/4圆围成的实体截面积，R=ef，

ef--翻边后边的厚度，

t—为材料厚度。

 因为         预冲孔孔径= D – 2ab

所以         当料厚  ≤0.5 时取ef = 1.0 t

                  当料厚   0.5 ＜t ＜0.8 时取ef = 0.7t

当料厚   t ≥0.8 时,取 ef = 0.6 t

 通常情况下取ef = 0.6 t .

     常用翻孔直径:

      M3    ￠2.5 (有屑加工)    ￠2.75 (无屑加工)

      M4    ￠3.3 (有屑加工)    ￠3.65 (无屑加工)

     无屑翻孔内径d = D-P/2 ,D为公称直径,P为螺距。

     一般情况下先冲预冲孔,在翻边,特殊情况下也可一次性翻边。

2.2 方形翻边的应用实例

    方形翻边的应用实例如图2所示。

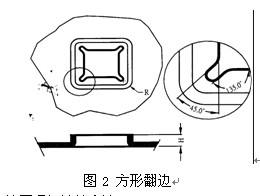
2.2.1方形翻边的计算原理与计算方法

原理：方形翻边，当翻边高度较高时,（H＞Hmax），直边部分展开与弯曲一致，圆角处展开按保留翻边的高度为H＝Hmax 的大小套弯曲公式展开，连接处用45度线及圆角均匀过渡，当翻边高度不高时（H≤Hmax）直边部分展开与弯曲一致，圆角处展开保留与直边一样的偏移植。

2.2．2  方形翻边的计算公式

     当R ≥4 mm 时：        材料厚度 t = 1.2 ～1.4 取Hmax = 4t

                              材料厚度 t = 0.8 ～1.0 取Hmax = 5t

                              材料厚度 t = 0.7 ～0.8 取Hmax = 6t

                              材料厚度 t ≤0.6       取Hmax = 8t

     当R ＜4 mm 时，需根据实验方法解决。

上述两例为通孔翻边的实例，下面两例为封闭异形（孔）翻边的实例。

2.3 压缩翻边（方形）的应用实例1

     压缩翻边（方形）的应用实例1如图3所示。

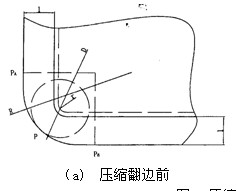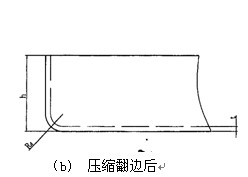
                             图3 压缩翻边1（R_d ≤1.5t）

图中h—为翻边后边高度，T—为料厚，Ra、r—为翻边后形成的内外圆弧半径，

     l—为翻边前模具刃口距坯料边缘的距离， D—为展开计算用圆弧直径，用来确定R′值，

R′--为坯料翻边前的圆弧半径。

2.3.1压缩翻边（方形）的计算原理与计算方法（R_d ≤1.5t）

原理：压缩翻边过程相当于一块平钢板，经过一次压力压缩成形后，形成底边与四条侧边围成的方形的封闭形体，而且在压缩成形时，每两条侧边交汇处同时压缩形成圆弧段R_d和r（由模具本身的冲头圆弧形状确定），图3（a)、（b)分别为压缩翻边前后的示意图，图3（a)为翻边的展开计算原理图，图（b)是省略表示的翻边后底边与两侧边围成的形体。

直边部分按弯曲展开，圆角部分按拉伸展开，然后用三点切圆（P_A-P-P_B）的方式作一段与两直边和直径为D的圆相切的圆弧。

2.3.2压缩翻边（方形）的计算公式

当R_d ≤1.5 t 时, 求D值计算公式如下:

D / 2 = ［（r + t / 3 ）²+ 2 （r + t / 3）× （h + t / 3）］^1/2

2.4  压缩翻边（方形）的应用实例2

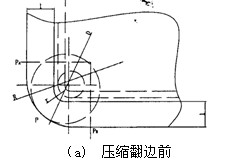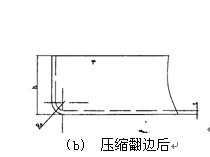
                           图4 压缩翻边2（R_d ＞1.5 t）

2.4.1压缩翻边（方形）的计算原理与计算方法（R_d ＞1.5 t）

原理：直边部分按弯曲展开，圆角部分按拉伸展开，然后用三点切圆（P_A-P-P_B）的方式作一段与两直边和直径为D的圆相切的圆弧。

本例的压缩成形过程和计算方法与上例一样，图4中出现的符号含义与上例一样。

2.4.2压缩翻边（方形）的计算公式

当R_d ＞1.5 t 时, 求D值计算公式如下:

D / 2 =｛（r + t/3 ）²+ 2 （r + t/3）×（h + t/3）-0.86×（R_d-2t/3）×

［（r + t/3）+0.16×（R_d-2t/3）］｝^1/2

3  结束语

本文对五金模具的形体翻边计算方法进行了论述,并结合几种比较复杂的翻边应用实例进行了计算说明,同时,推导出相应的设计计算公式,仅供模具设计人员参考，模具设计人员可以直接采用上述翻边计算公式进行有关计算工作。

参  考  文  献

［1］冯炳尧 韩素荣 蒋文森. 模具设计与制造简明手册. 上海科学技术出版社. 1999.

［2］万战胜  . 冲压工艺及模具设计. 中国铁道出版社. 1995.

作者简介：黄义俊（1959-），男，高级工程师/副教授，模具设计与制造专业，长期从事

冲压模具、塑料模具设计与机械产品设计方面的科研与教学工作。

浙江省宁波市北仑区新大路1069号,315800